Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 1.10 : Common Graphs
14. Without using a graphing calculator sketch the graph of \({x^2} - 4x + {y^2} - 6y - 87 = 0\).
Hint : Complete the square a couple of times to put this into standard from. This will allow you to identify the type of graph this will be.
The first thing that we should do is complete the square on the \(x\)’s and the \(y\)’s to see what we’ve got here. This could be a circle, ellipse, or hyperbola and completing the square a couple of times will put it into standard form and we’ll be able to identify the graph at that point.
Here is the completing the square work.
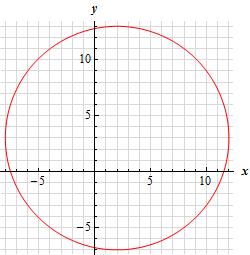
\[\begin{align*}{x^2} - 4x + \left( {4 - 4} \right) + {y^2} - 6y + \left( {9 - 9} \right) - 87 & = 0\\ {\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} - 100 & = 0\\ {\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} & = 100\end{align*}\]So, we’ve got a circle with center \(\left( {2,3} \right)\) and radius 10. Here is a sketch of the circle.